论文题目:Generalized Birch lemma and the 2-part of the Birch and Swinnerton-Dyer conjecture for certain elliptic curves
论文作者:Jie Shu, Shuai Zhai.
发表刊物:Journal für die reine und angewandte Mathematik
成果介绍:In the present paper, we generalize the celebrated classical lemma of Birch and Heegner on quadratic twists of elliptic curves over 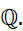 We prove the existence of explicit infinite families of quadratic twists with analytic ranks 0 and 1 for a large class of elliptic curves, and use Heegner points to explicitly construct rational points of infinite order on the twists of rank 1. In addition, we show that these families of quadratic twists satisfy the 2-part of the Birch and Swinnerton-Dyer conjecture when the original curve does. We also prove a new result in the direction of the Goldfeld conjecture. All these results apply to a large class of elliptic curves, especially for elliptic curves without CM. As applications, we present examples of elliptic curves of small conductors, of Newmann-Setzer curves and also examples of elliptic curves without CM for which the full Birch and Swinnerton-Dyer conjecture holds.
We prove the existence of explicit infinite families of quadratic twists with analytic ranks 0 and 1 for a large class of elliptic curves, and use Heegner points to explicitly construct rational points of infinite order on the twists of rank 1. In addition, we show that these families of quadratic twists satisfy the 2-part of the Birch and Swinnerton-Dyer conjecture when the original curve does. We also prove a new result in the direction of the Goldfeld conjecture. All these results apply to a large class of elliptic curves, especially for elliptic curves without CM. As applications, we present examples of elliptic curves of small conductors, of Newmann-Setzer curves and also examples of elliptic curves without CM for which the full Birch and Swinnerton-Dyer conjecture holds.
所属学科:基础数学
论文地址:https://www.degruyter.com/document/doi/10.1515/crelle-2021-0004/html
 Official wechat
Official wechat
 中文版
中文版